Using Regression Tree to Solve Regression Problems
The Regression Tree task can build a regression model using the decision tree approach.
The output of the task is a tree structure, and a set of intelligible rules, which can be analyzed in the Rule Manager.
Prerequisites
the required datasets have been imported into the process
the data used for the model has been well prepared, and includes a categorical output and a number of inputs. Data preparation may involve discretization before building the decision tree, to improve the accuracy of the model and to reduce the computational effort.
a single unified dataset has been created by merging all the datasets imported into the process.
Additional tabs
Along with the Options tab, where the task can be configured, the following additional tabs are provided:
Documentation tab where you can document your task,
Parametric options tab where you can configure process variables instead of fixed values. Parametric equivalents are expressed in italics in this page (PO).
Monitor and Results tabs, where you can see the output of the task computation. See Results table below.
Procedure
Drag and drop the Regression Tree task onto the stage.
Connect a task, which contains the attributes from which you want to create the model, to the new task.
Double click the Regression Tree task.
Configure the options described in the table below.
Save and compute the task.
Regression Tree options | ||
Parameter Name | PO | Description |
|---|---|---|
Input attributes | inpnames | Drag and drop the input attributes which will be used to generate predictive rules in the decision tree. |
Output attributes | outnames | Drag and drop the attributes which will contain the results of the predictive analysis. |
Minimum number of patterns in a leaf | npattnode | The minimum number of patterns that a leaf can contain. If a node contains less than this threshold, tree growth is stopped and the node is considered a leaf. |
Maximum impurity in a leaf | maximpur | Specify the threshold on the maximum impurity in a node. The impurity is calculated with the method selected in the Impurity measure option. By default this value is zero, so trees grow until a pure node is obtained (if possible with training set data) and no ambiguities remain. |
Pruning method | treepruning | The method used to prune redundant leaves after tree creation. The following choices are currently available:
|
Method for handling missing data | treeusemissing | Missing data can be handled using one of the following methods:
|
Select the attribute to split before the value | selattfirst | If selected, the QUEST method is used to select the best split. According to this approach, the best attribute to split is selected via a correlation measure, such as F-test or Chi-Square. After choosing the best attribute, the best value for splitting is selected. |
Aggregate data before processing | aggregate | If selected, identical patterns are aggregated and considered as a single pattern during the training phase. |
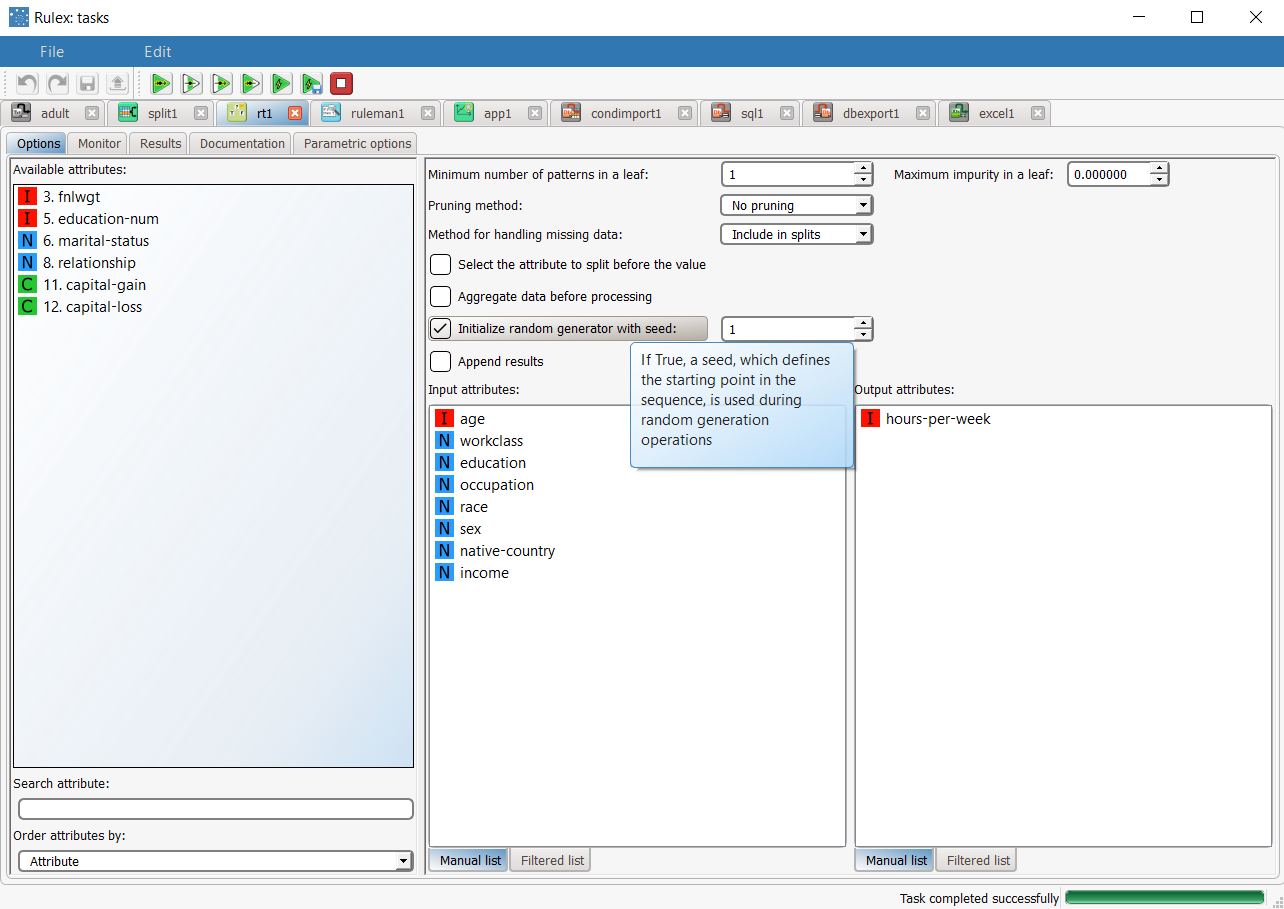
Initialize random generator with seed | initrandom, iseed | If selected, a seed, which defines the starting point in the sequence, is used during random generation operations. Consequently using the same seed each time will make each execution reproducible. Otherwise, each execution of the same task (with same options) may produce dissimilar results due to different random numbers being generated in some phases of the process. |
Append results | append | If selected, the results of this computation are appended to the dataset, otherwise they replace the results of previous computations. |
Results
The results of the Regression Tree task can be viewed in two separate tabs:
The Monitor tab, where it is possible to view the statistics related to the generated rules as a set of histograms, such as the distribution of the number of conditions, covering and error. Rules relative to different classes are displayed as bars of a specific color. These plots can be viewed during and after computation operations.
The Results tab, where statistics on the RT computation are displayed, such as the execution time, number of rules etc.
Example
The following examples are based on the Adult dataset.
Scenario data can be found in the Datasets folder in your Rulex installation.
The scenario aims to solve a simple regression problem based on the hours per week people statistically work, according to such factors as their age, occupation and marital status.
The following steps were performed:
First we import the adult dataset with an Import from Text File task.
Split the dataset into a test and training set with a Split Data task.
Generate rules from the dataset using the Decision Tree task.
Analyze the generated rules with a Rule Manager task.
Apply the rules to the dataset with an Apply Model task.
View the results of the forecast via the Take a look functionality.
Procedure | Screenshot |
|---|---|
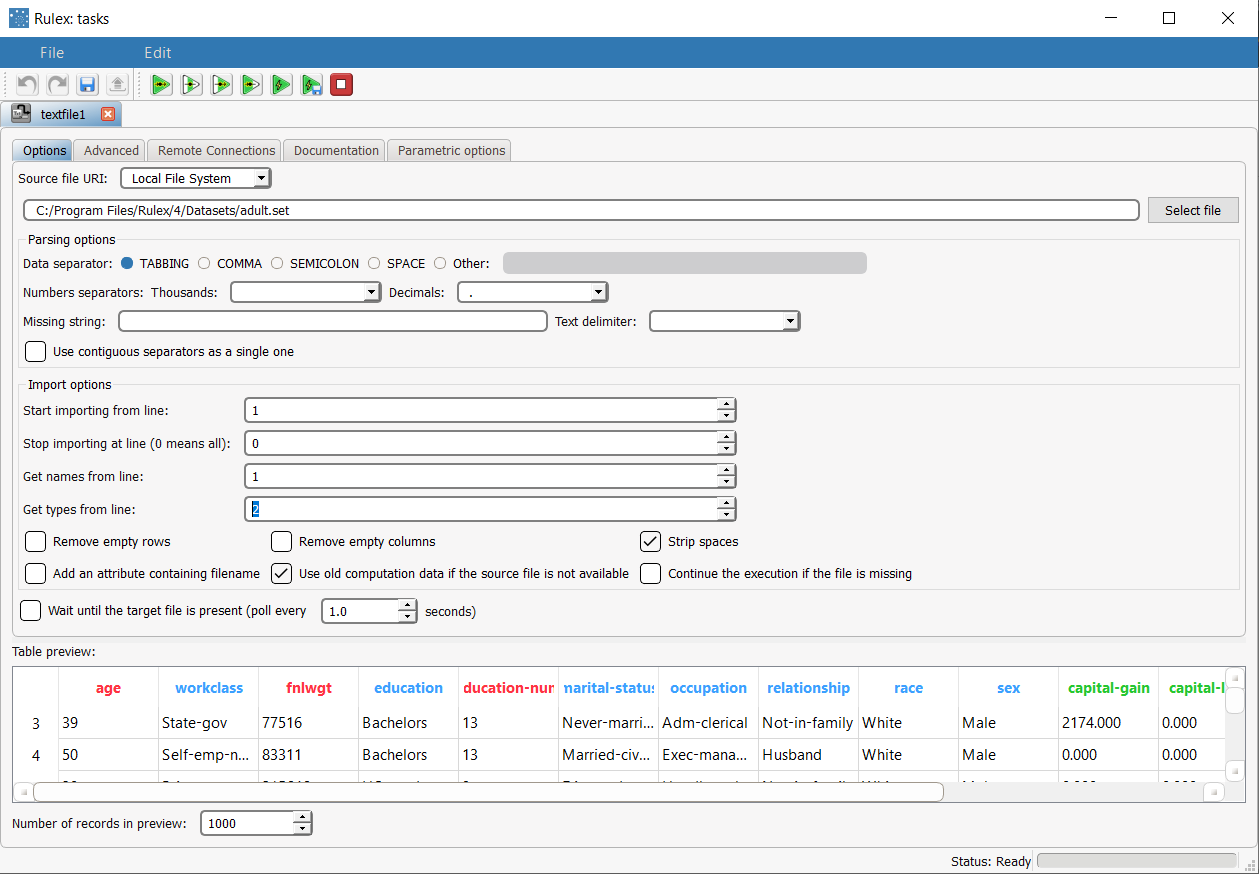
Import the adult dataset with the Import from Text File task, and specify that the second line defines the attribute type. | Note that this regression problem in completely different from the NN classification problem, where income was the output. In this regression example, we are not particularly interested in the physical meaning of this analysis, but only want to illustrate the potentiality of regression in a real-world dataset. |
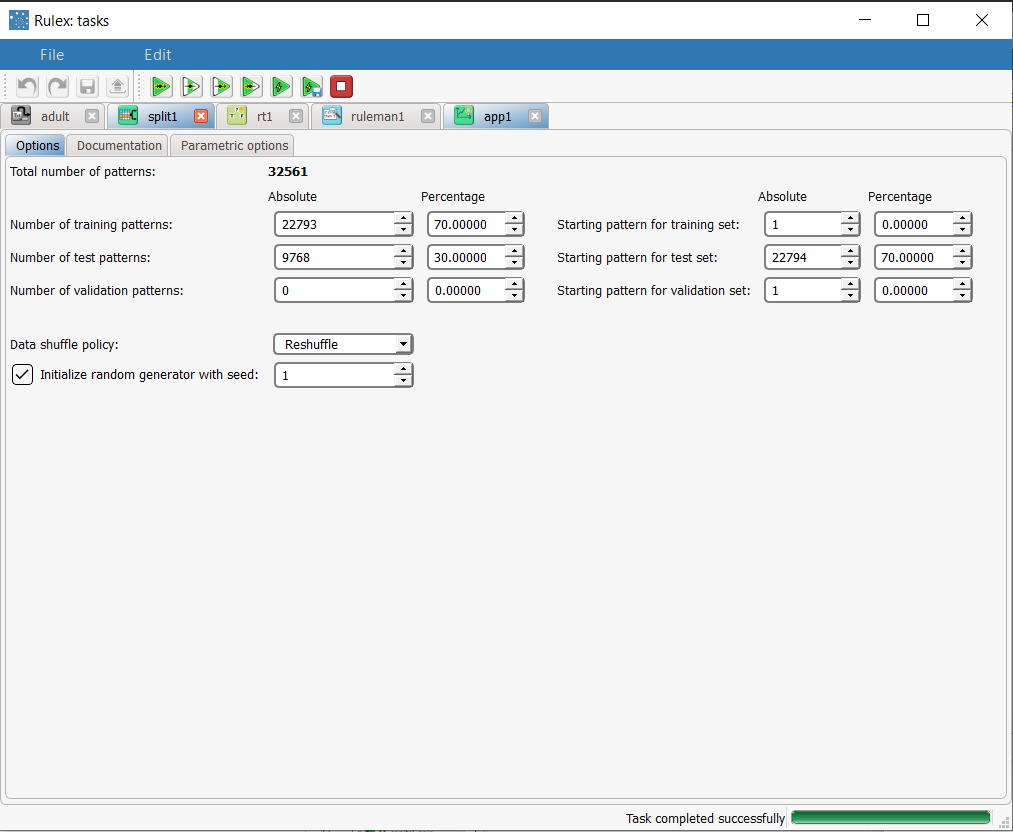
Add a Split Data task, and split the dataset into test (30%) and training (70%) sets. | |
Add a Regression Tree task to the process, and double click to open it. As this is a regression task, we need an ordered output, so we define the hours-per-week attribute as the output attribute. Drag and drop the following attributes onto the Input attributes pane:
| |
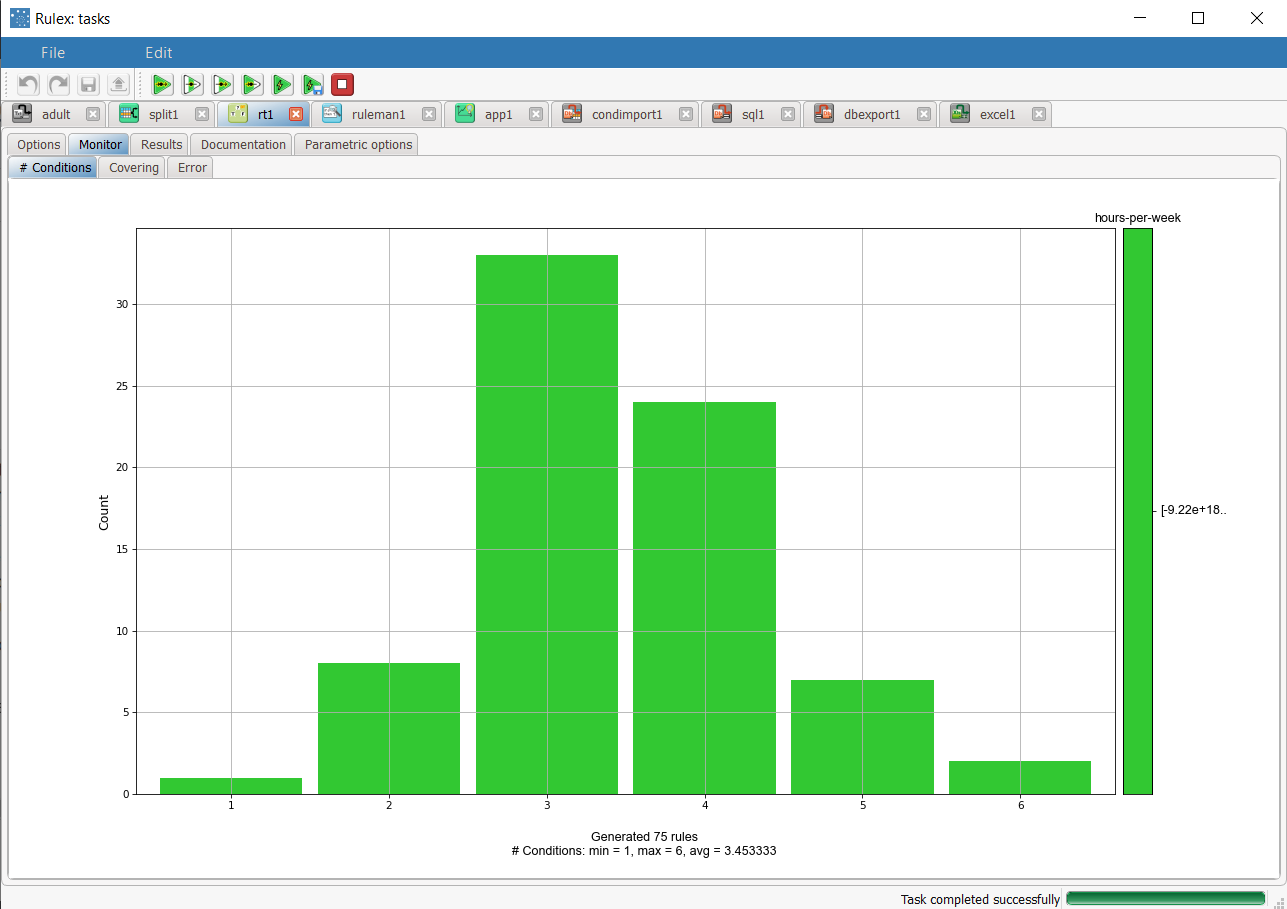
Click Compute process to start the analysis: the properties of the generated rules can be viewed in the Monitor tab of the RT task, in particular at the end of the process the number of conditions of the rules are distributed as follows :
The total number of rules, and the minimum, maximum and average of the number of conditions is reported, too. Analogous histograms can be viewed for covering and error, by clicking on the corresponding tabs. | |
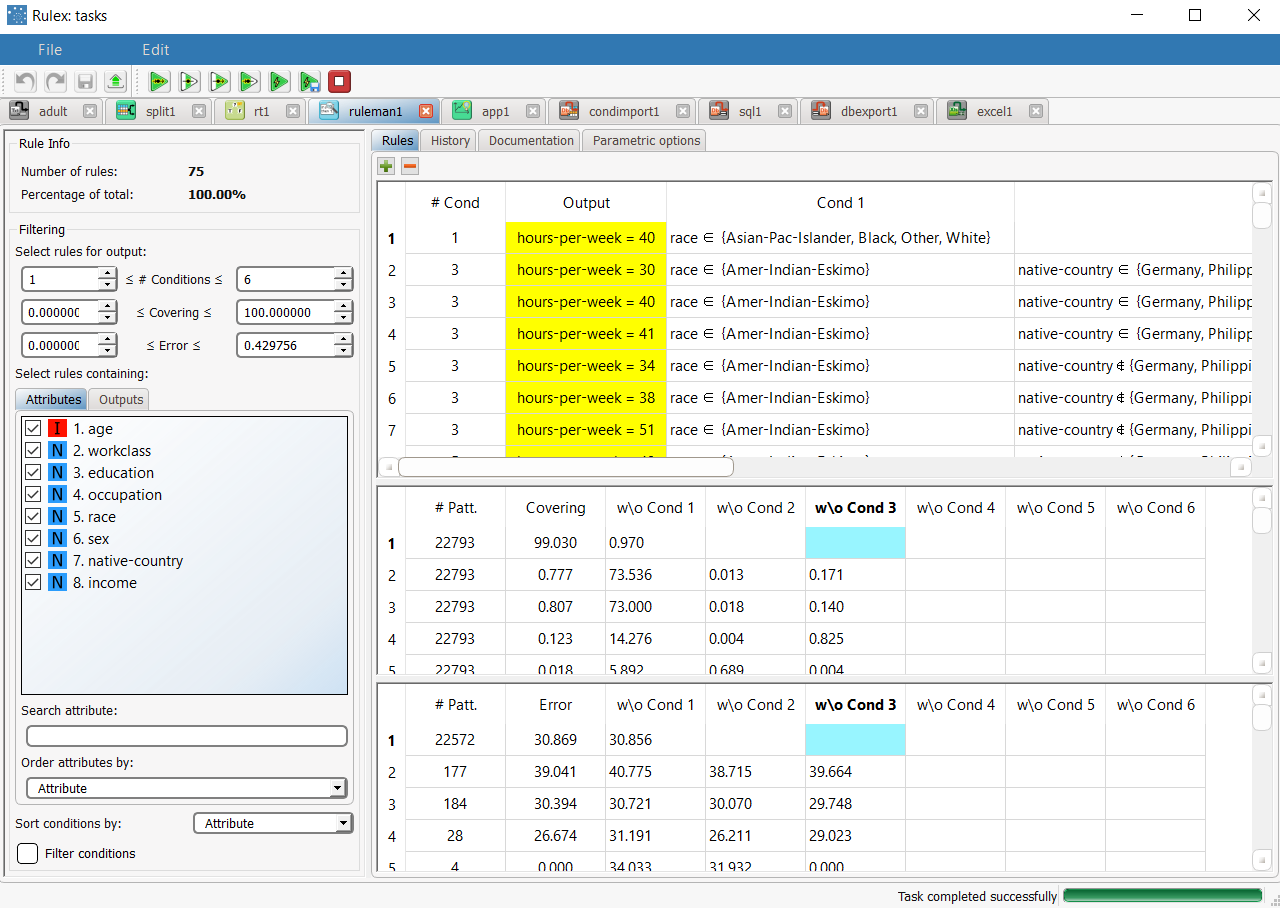
The rule spreadsheet that can be viewed by adding a Rule Manager task to the process. For example, rule 1 states that if material-status is in the set {Asian-Pac-Islander, Black, Other, White} then the corresponding hours-per-week is 40. The total number of generated rules is 75. | |
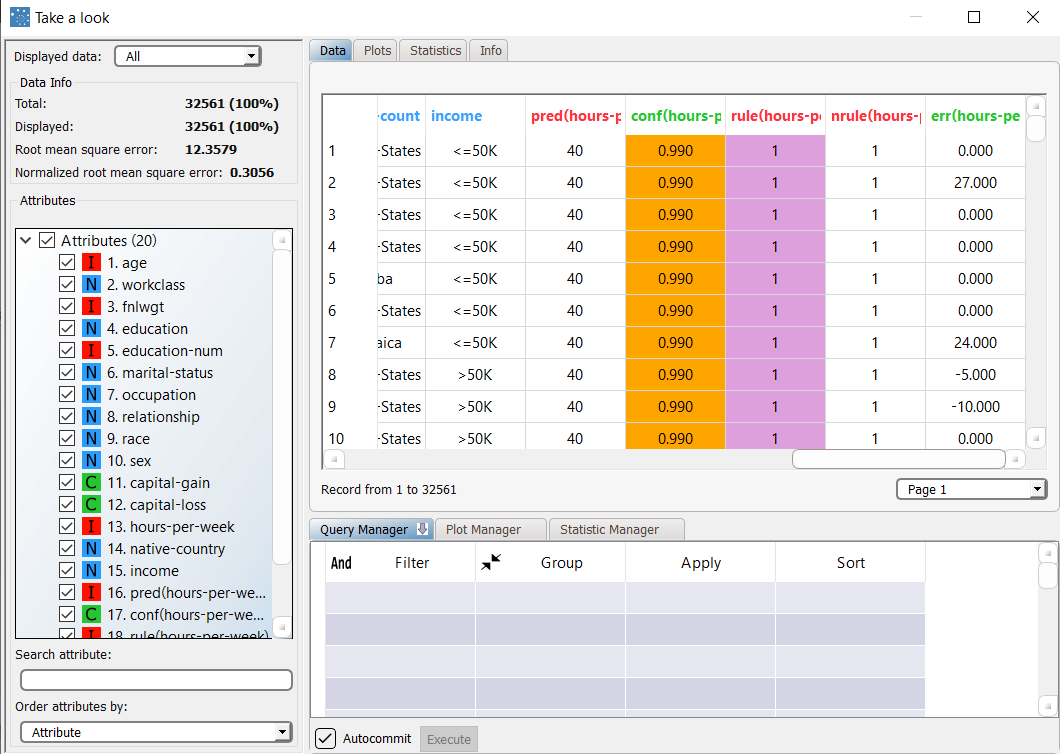
We can check out the application of this set of rules to the training and test patterns by adding an Apply Model task, and computing it with the default options. Right-clicking the computed task, and selecting Take a look allows us to check out the results. The application of the rules generated by the Regression Tree task has added four columns containing:
The content of the parentheses is the name of the variable the prediction refers to. From the summary panel on the left we can see that the model scores a 12.35 of mean square error in the training set. | |
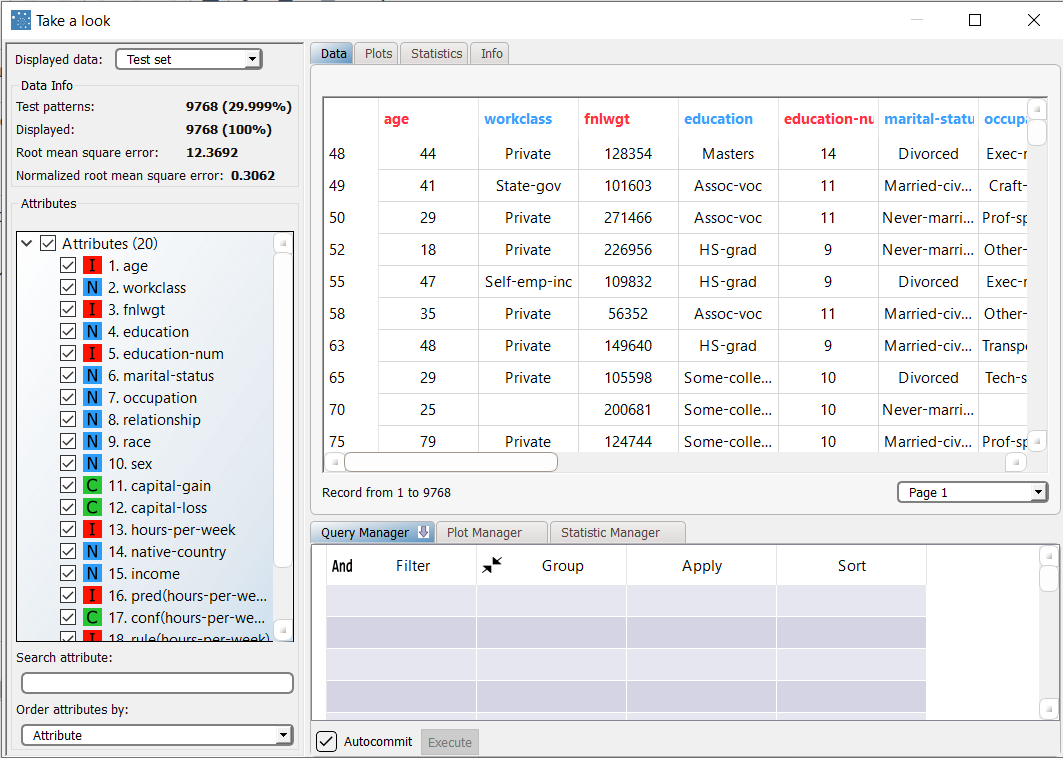
Selecting Test Set from the Displayed data drop down list shows how the rules behave on new data. In the test set, the normalized mean square error is about 12.36. |