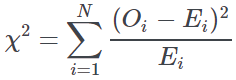General parameters

Use missing values

Check to include missing values as a separate category in the analyses.

Sample size

Number of total valid samples

The number of valid data samples for both attributes n is displayed.

This is particularly useful when there is a heavily unbalanced distribution of missing data among the two attributes, which might cause the analysis to be based on an unacceptably small sample size.

Contingency tables

Contingency table

Data are tabulated into a contingency table, which includes the number of observed counts.

Expected contingency table

A table of the expected counts under the hypothesis of no association between the two attributes is produced.

For example, expected counts for the cell a_ij are obtained by the product of the total count for the row i and the total count for the column j, divided by the total number of elements inside the table.

Statistical test

Pearson chi square

The Pearson chi square test χ² is performed for the association between the two attributes.

The test is based on the difference between the observed count (O) in each cell and the corresponding expected value (E) under the null hypothesis of no association.

For example in the presence of a cross-tabulation table containing m rows, n columns and N=mn cells:

Where, under the null hypothesis , χ² is assumed to follow a chi square distribution with (m−1)(n−1) degrees of freedom.

Statistical test

P-value for Pearson chi square

A p-value for the Pearson chi square test is also provided, which calculates the lowest level of significance at which the null hypothesis of the coefficient would be rejected. Consequently the smaller the p-value the stronger the evidence in favor of the alternative hypothesis.