Using LLM to Solve Regression Problems
Rulex solves regression problems with the Regression Logic Learning Machine task (LLM).
This task accurately predicts continuous variables, for example, predicting the price of goods, given a set of input attributes on market conditions, through predictive intelligible logic based rules.
Prerequisites
the required datasets have been imported into the process
the data used for the model has been well prepared
a single unified dataset has been created by merging all the datasets imported into the process.
Additional tabs
The following additional tabs are provided:
Documentation tab where you can document your task,
Parametric options tab where you can configure process variables instead of fixed values. Parametric equivalents are expressed in italics in this page (PO).
Monitor & Results tabs, where you can see the output of the task computation. See Results table below.
Procedure
Drag and drop the Logic Learning Machine task onto the stage.
Connect a task, which contains the attributes from which you want to create the model, to the new task.
Double click the Logic Learning Machine task. The left-hand pane displays a list of all the available attributes in the dataset, which can be ordered and searched as required.
Configure the options described in the table below.
Save and compute the task.
Regression LLM options | ||
Parameter Name | PO | Description |
|---|---|---|
Aggregate data before processing | aggregate | If selected, identical patterns are aggregated and considered as a single pattern during the training phase. |
Minimize number of conditions | minimal | If selected, rules with fewer conditions, but the same covering, are privileged. |
Perform a coarse-grained training | lowest | If selected, the LLM training algorithm considers the conditions with the subset of values that maximizes covering for each input attribute. Otherwise, only one value at a time is added to each condition, thus performing a more extensive search. The coarse-grained training option has the advantage of being faster than performing an extensive search. |
Prevent interval conditions for ordered attributes | nointerval | If selected, interval conditions such as 1<x≤5 are avoided, and only conditions with > (greater than) ≤ (lower or equal than) are generated. |
Ignore attributes not present in rules | reducenames | If selected, attributes that have not been included in rules will be flagged Ignore at the end of the training process, to reflect their redundancy in the classification problem at hand. |
Hold all the generated rules | holdrules | If selected, even redundant generated rules, which are verified only by training samples that already covered by other more powerful rules, are kept. |
Use median as output value | usemedian | If selected, the median is used instead of the average when computing the output of each rule. |
Consider relative error instead of absolute | relerrmax | Specify whether the relative or absolute error must be considered. The Maximum error allowed for each rule is set by considering proportions of samples belonging to different classes. Imagine a scenario where for given rule pertaining to the specific output value yo:
In this scenario the absolute error of that rule is FP/(TN+FP), whereas the relative error is obtained as follows: FP/Min(TP+FN,TN+FP) (samples with the output value yo that do verify the conditions of the rule). |
Maximum number of trials in bottom-up mode | nbuiter | The number of times a bottom-up procedure can be repeated, after which a top-down procedure will be adopted. The bottom-up procedure starts by analyzing all possible cases, defining conditions and reducing the extension of the rules. If, at the end of this procedure, the error is higher than the value entered for the Maximum error allowed for each rule (%) option, the procedure starts again, inserting an increased penalty on the error. If the maximum number of trials is reached without obtaining a satisfactory rule, the procedure is switched to a top-down approach. |
Maximum desired dispersion coefficient | maxsdev | The maximum dispersion coefficient of the output points contained in the rule. The higher the dispersion the more generic the rules. |
Overlap between rules (%) | maxoverlap | Set the maximum percentage of patterns, which can be shared by two rules. |
Maximum nominal values | maxnomval | Set the maximum number of nominal values that can be contained in a condition. This is useful for simplifying conditions and making them more manageable, for example when an attribute has a very high number of possible nominal values. It is worth noting that overly complicated conditions also run the risk of over-fitting, where rules are too specific for the test data, and not generic enough to be accurate on new data. |
Number of rules for each class (0 means 'automatic') | numrules | If set to 0 the minimum number of rules required to cover all patterns in the training set is generated. Otherwise set the desired number of rules for each class. |
Initialize random generator with seed | initrandom, iseed | If selected, a seed, which defines the starting point in the sequence, is used during random generation operations. Consequently using the same seed each time will make each execution reproducible. Otherwise, each execution of the same task (with same options) may produce dissimilar results due to different random numbers being generated in some phases of the process. |
Maximum error in classification sub-problems (%) | errmax | Maximum percentage of errors allowed when building rules that distinguish between the clustered and non-clustered points. A value higher than 0 could increase dispersion of rules. |
Append results | append | If selected, the results of this computation are appended to the dataset, otherwise they replace the results of previous computations. |
Maximum number of conditions for a rule | maxant | Set the maximum number of conditions in a rule. |
Missing values verify any rule condition | missrelax | If selected, missing values will be assumed to satisfy any condition. If there is a high number of missing values, this choice can have an important impact on the outcome. |
Key Attributes | keynames | Drag and drop here the key attributes. Rulex will create a different set of rules for each key attribute value. Instead of manually dragging and dropping attributes, they can be defined via a filtered list. Key attributes are the attributes that must always be taken into consideration in rules, and every rule must always contain a condition for each of the key attributes. |
Results
The results of the LLM task can be viewed in two separate tabs:
The Monitor tab, where it is possible to view the statistics related to the generated rules as a set of histograms, such as the number of conditions, covering value, or error value. Rules relative to different classes are displayed as bars of a specific color. These plots can be viewed during and after computation operations.
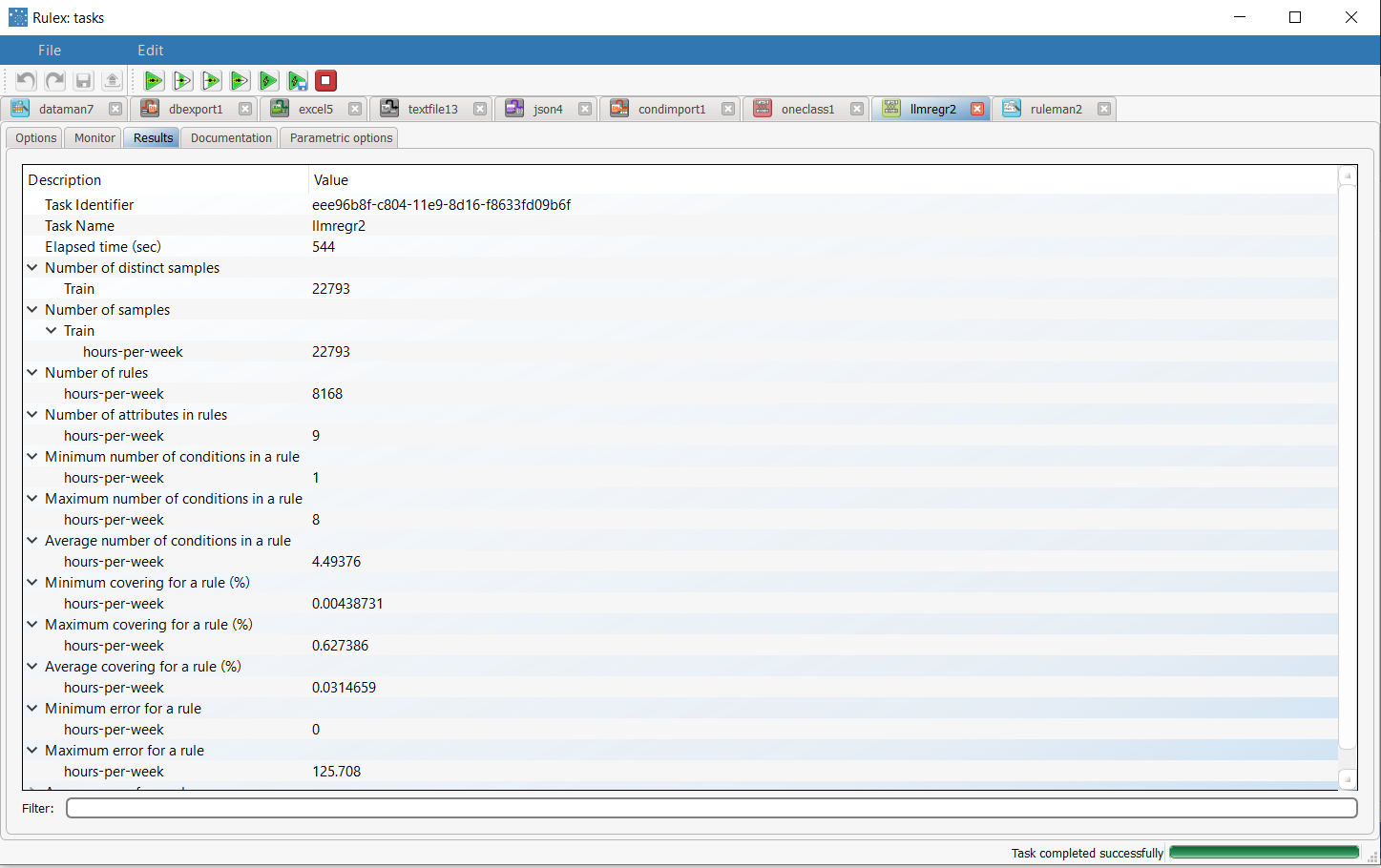
The Results tab, where statistics on the LLM computation are displayed, such as the execution time, number of rules, average covering etc.
Example
The following examples are based on the Adult dataset.
Scenario data can be found in the Datasets folder in your Rulex installation.
The scenario aims to solve a simple regression problem based on the hours per week people statistically work, according to such factors as their age, occupation and marital status.
The following steps were performed:
First we import the adult dataset with an Import from Text File task.
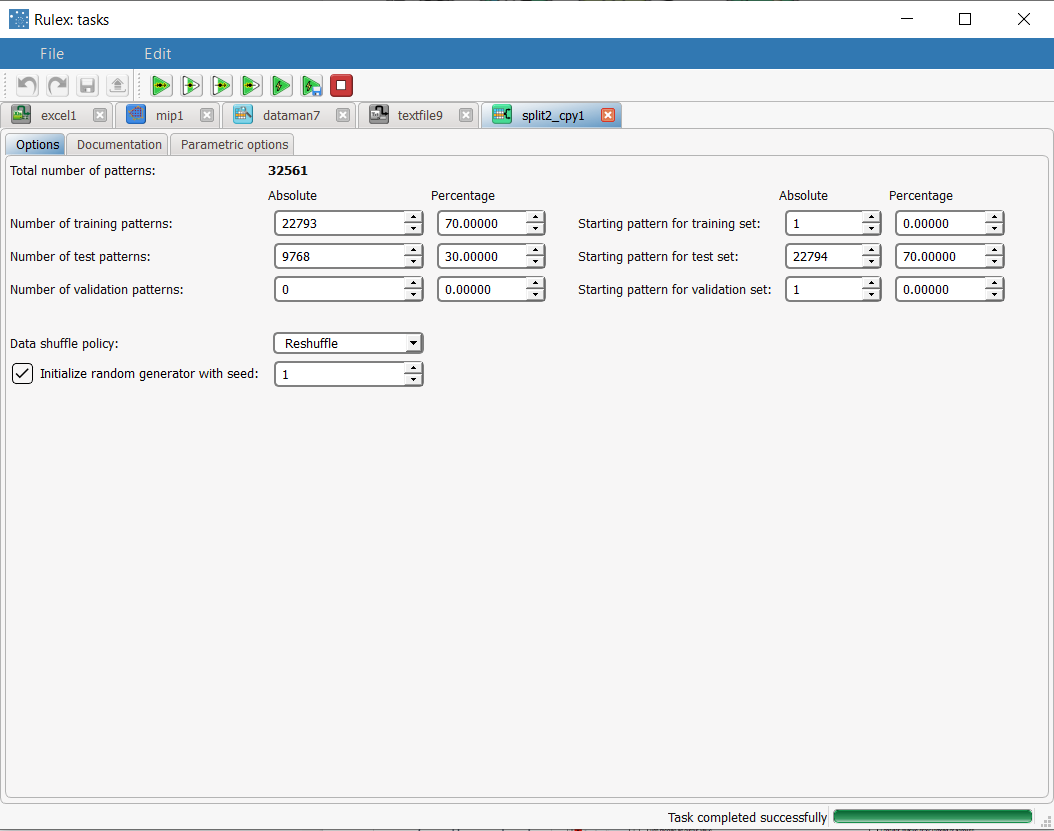
Split the dataset into a test and training set with a Split Data task.
Generate rules from the dataset with the Regression LLM.
Analyze the generated rules with a Rule Manager task.
Apply the rules to the dataset with an Apply Model task.
View the results of the forecast with a Data Manager task.
Procedure | Screenshot |
|---|---|
After importing the Adult dataset with the Import from Text File task, add a Split Data task to split the data into test (30%) and training (70%) datasets. | |
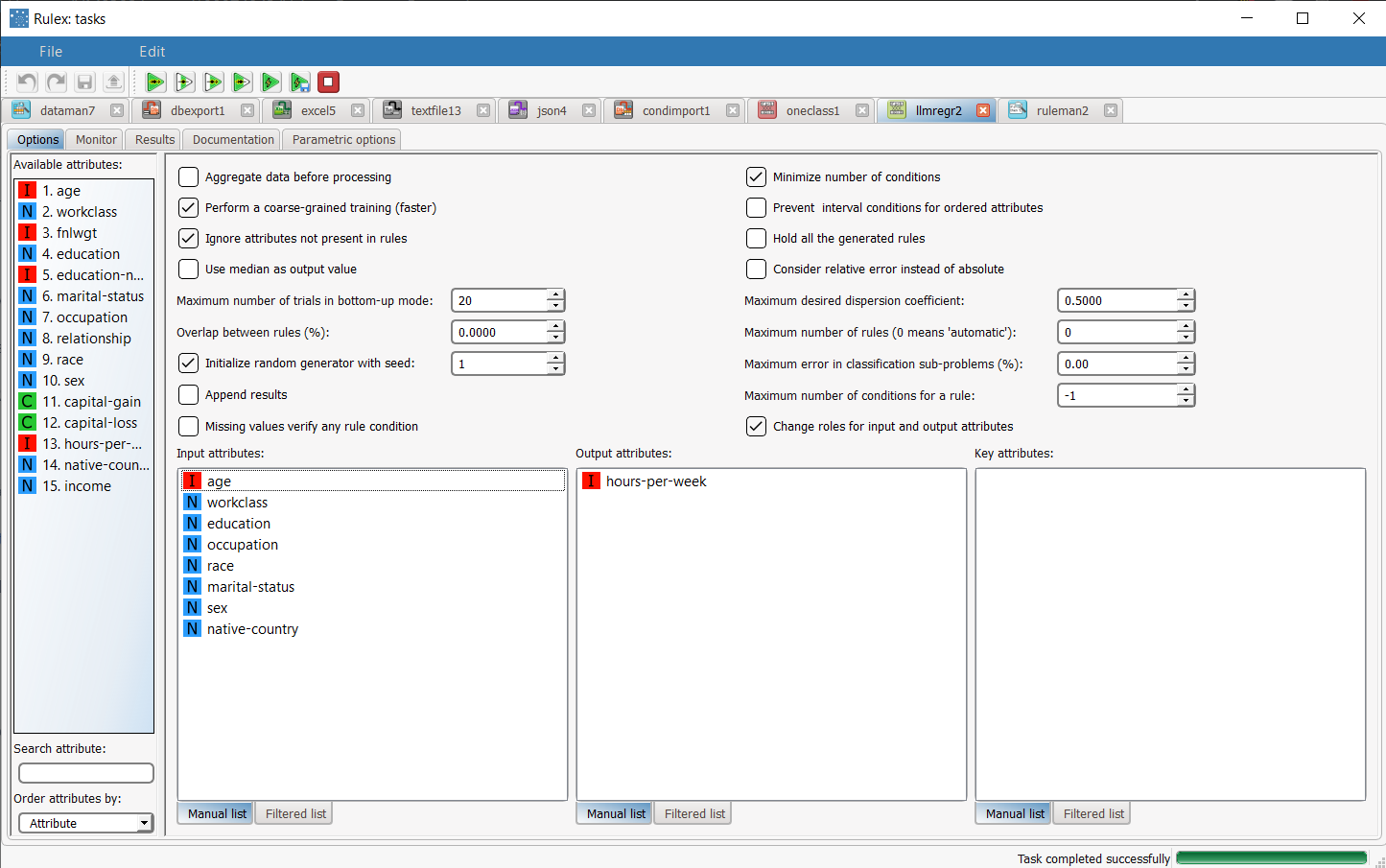
Then add a Regression LLM task to the process, specify hours-per-week as the output attribute, and the following attributes as input attributes:
Then save and compute the task. | |
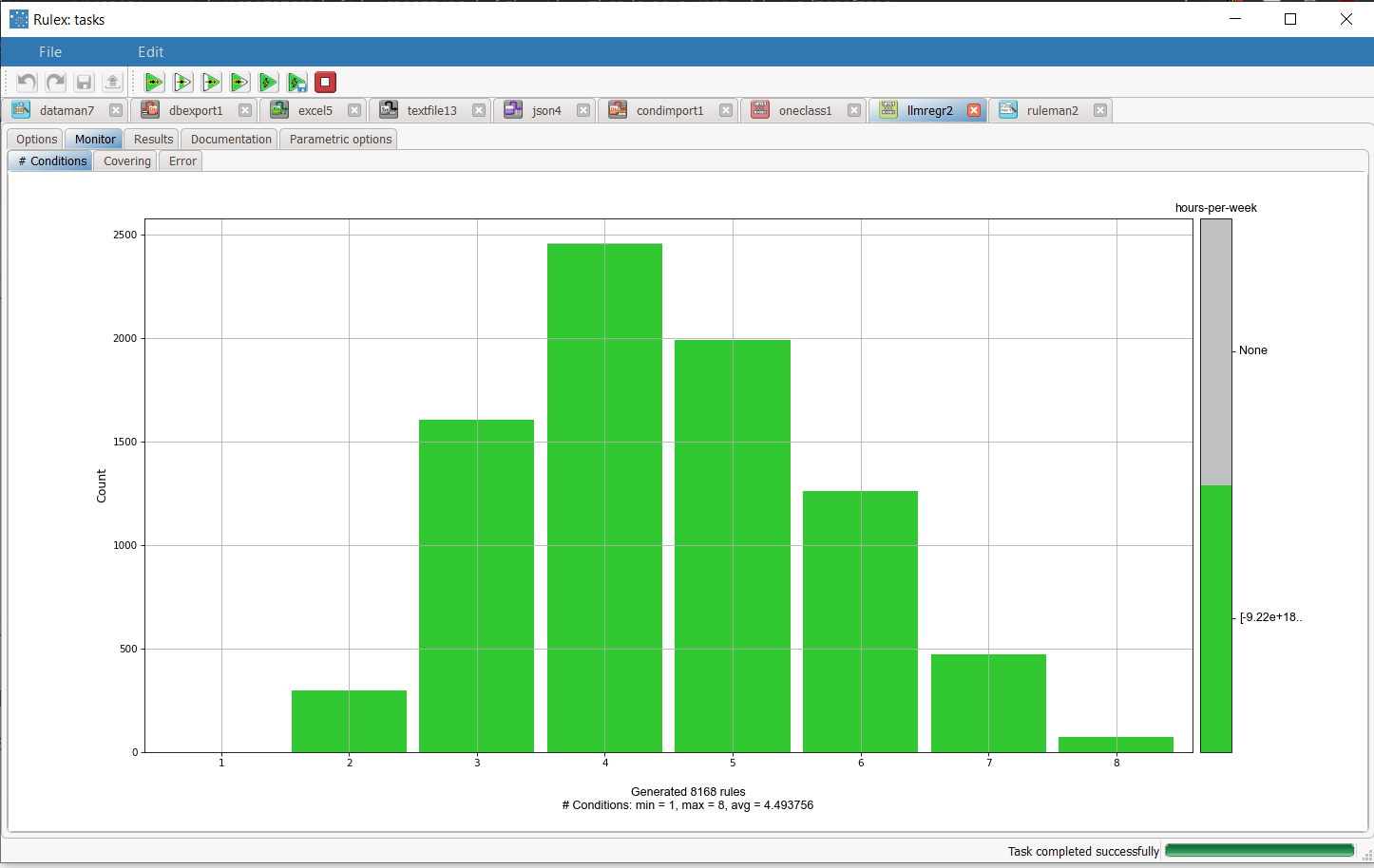
The distribution and properties of the generated rules can be viewed in the Monitor tab of the LLM task. For example, there are 2458 rules with 4 conditions. The total number of rules, and the minimum, maximum and average of the number of conditions is reported, too. Analogous histograms can be viewed for covering and error, by clicking on the corresponding tabs. | |
Clicking on the Results tab displays a great deal of information on the task, such as
| |
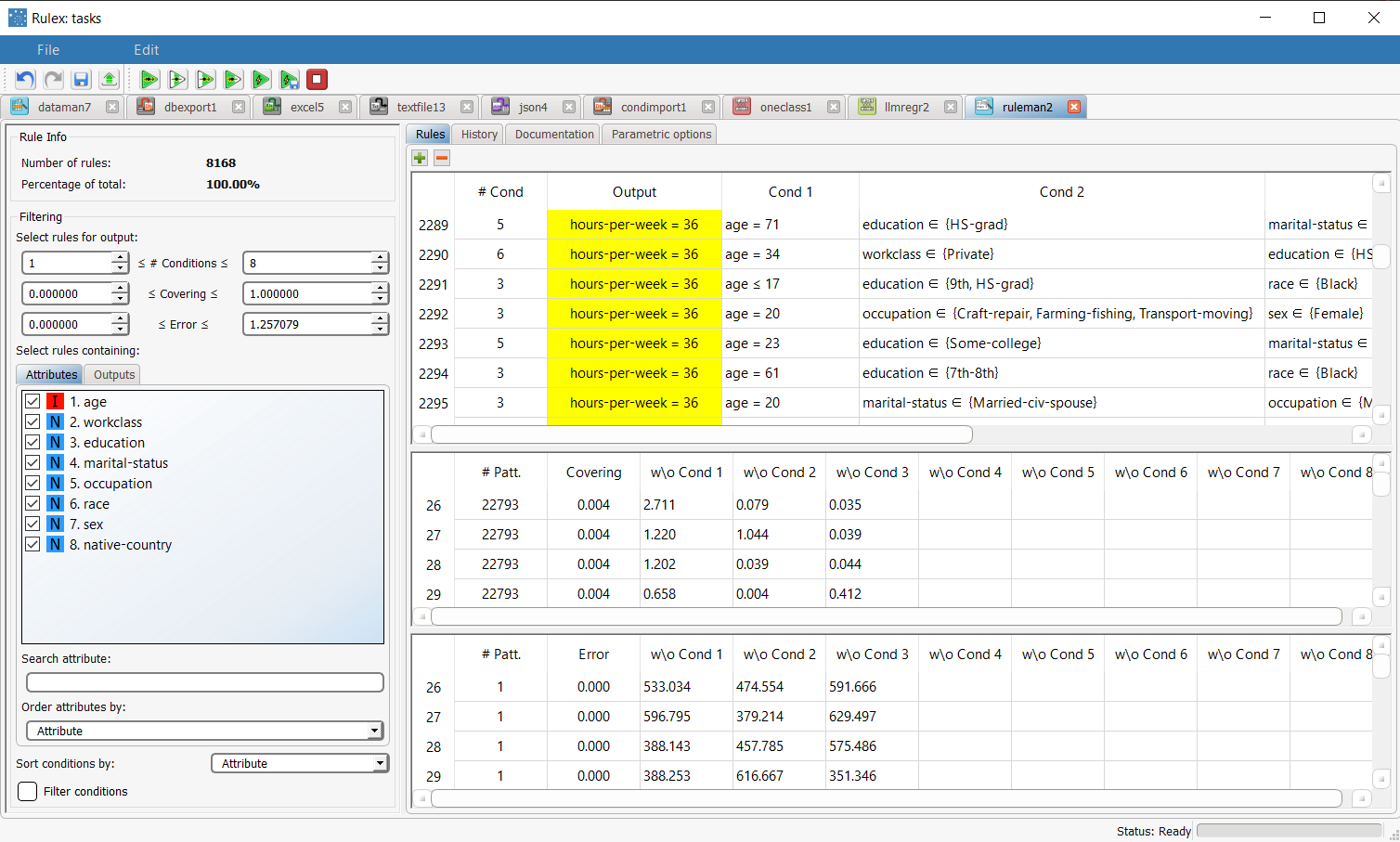
The rule spreadsheet that can be viewed by double-clicking on the Rule Manager task is initially ordered by output value. For example, rule 2292 states that if age is 20 and occupation is in the set {Craft-repair, Farming-fishing, transport-moving} and sex is Female then hours-per-week is 36. | |
The forecast ability of the set of rules resulting from LLM can be viewed by adding an Apply Model task to the process, and computing it with default values. | |
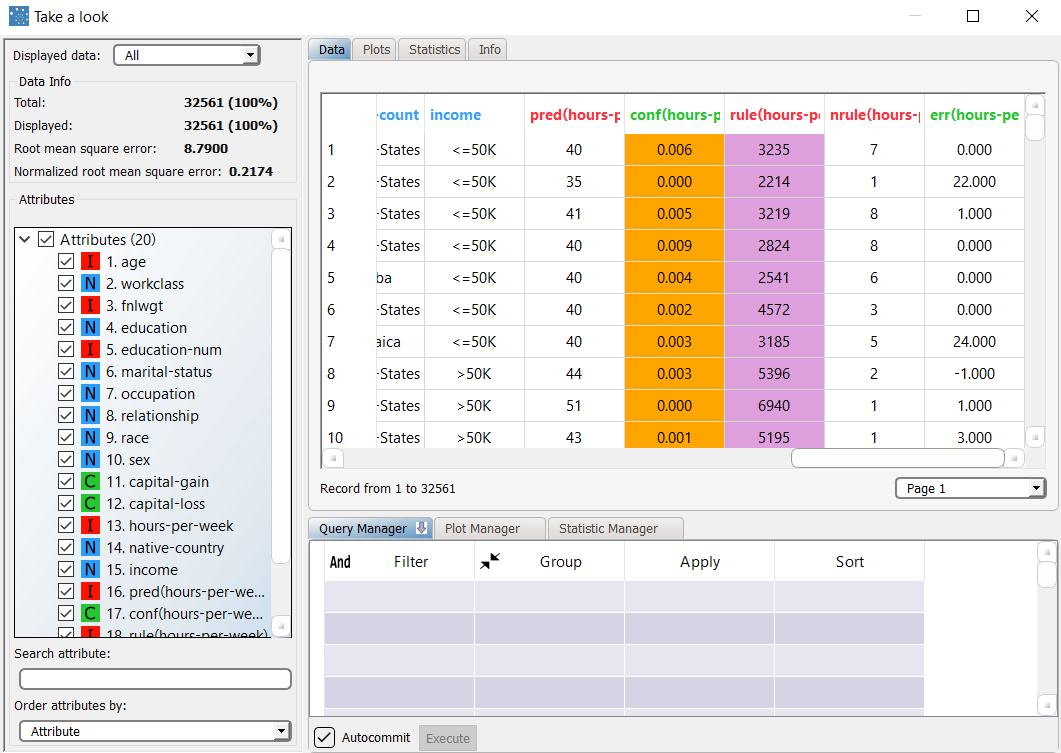
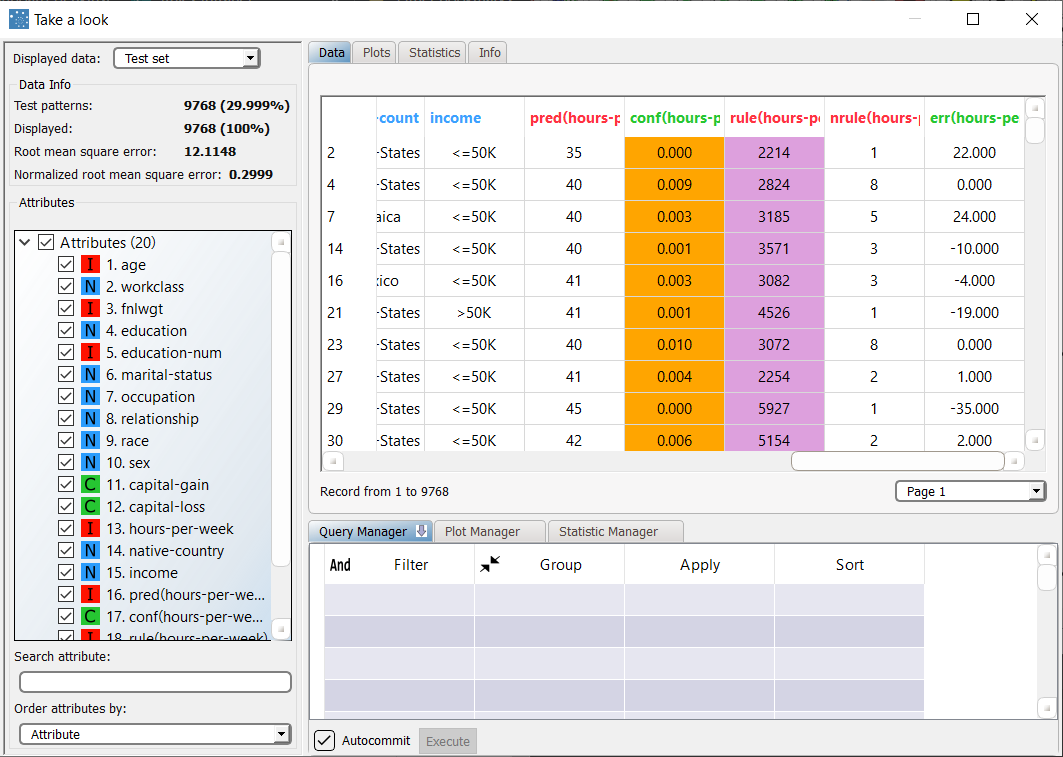
Right-click the computed Apply Model task and select Take a look, to check the results. The following columns have been added to the data set:
| From the summary panel on the left we can see that the LLM regression model scores a root mean square error (RMSE) of 8.7900 in the training set. |
Selecting Test Set from the Displayed data drop down list shows how the rules behave on new data. In the test set, the value of RMSE is 12.1148, slightly higher than the overall score. |