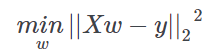Using Linear to Solve Regression Problems
The Linear solves regression problems in which the output value is expected to be a linear combination of the input variables through the Ordinary Least Squares (OLS) method.
In mathematical notion, if ŷ is the predicted output value and 𝓍1,...,𝓍d the input variables, we want to find the weights vector 𝓌0,𝓌1,...,𝓌d such that ŷ=𝓌0+𝓌1𝓌1+...+𝓌d𝓍d.
The weights 𝓌1,...𝓌d are called coefficients, while 𝓌0 is the intercept or constant term.
Weights are computed in order to minimize the residual sum of squares between the input patterns in the dataset, and the responses predicted by the linear approximation. Mathematically this task solves a problem in the form:
The output of the task is the weights vector 𝓌0,𝓌1,...,𝓌d.
Prerequisites
the required datasets have been imported into the process
the data used for the model has been well prepared, and contains a discrete or continuous output and a number of inputs.
a single unified dataset has been created by merging all the datasets imported into the process.
Additional tabs
Along with the Options tab, where the task can be configured, the following additional tabs are provided:
Documentation tab where you can document your task.
Parametric options tab where you can configure process variables instead of fixed values. Parametric equivalents are expressed in italics in this page (PO).
Coefficients and Results tabs, where you can see the output of the task computation. See Results table below.
Procedure
Drag and drop the Linear task onto the stage.
Connect a task, which contains the attributes from which you want to create the model, to the new task.
Double click the Linear task.
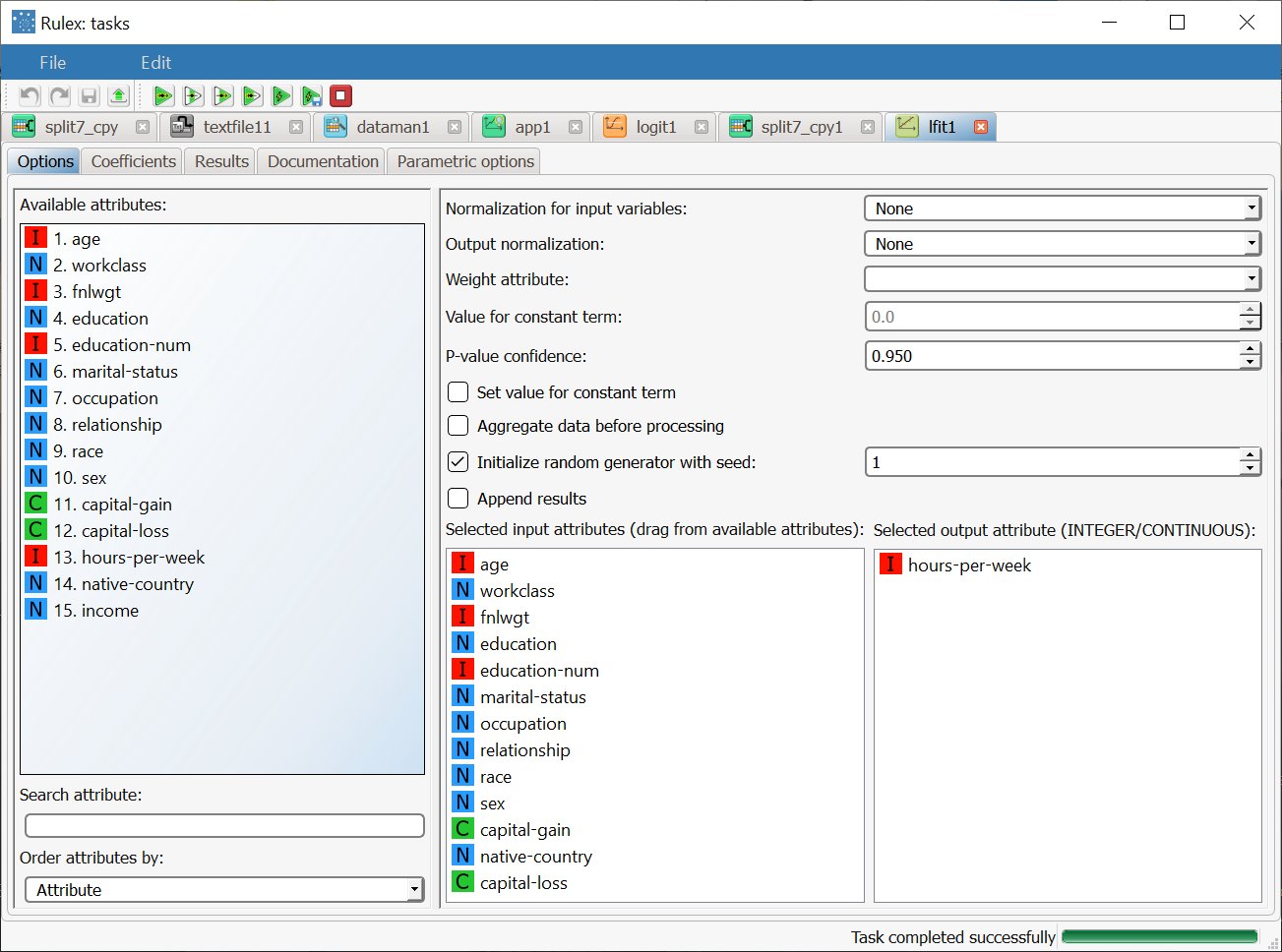
Drag and drop the input attributes, which will be used for regression, from the Available attributes list on the left to the Selected input attributes list.
Drag and drop the integer and/or continuous output attributes, which will be used for regression, from the Available attributes list on the left to the Selected output attribute list.
Configure the options described in the table below.
Save and compute the task.
Linear options | ||
Parameter Name | PO | Description |
|---|---|---|
Normalization of input variables | normtype | The type of normalization to use when treating ordered (discrete or continuous) variables. Possible methods are:
Every attribute can have its own value for this option, which can be set in the Data Manager task. These choices are preserved if Attribute is selected in the Normalization of input variables option; otherwise any selections made here overwrite previous selections made. Normalization types For further info on possible types see Managing Attribute Properties |
Output normalization | normout | Select which method should be adopted to normalize output variables. Possible types are the same as those provided for input variables. |
Weight attribute | linfitweightname | If specified, this attribute represents the relevance (weight) of each sample (i.e., of each row) with respect to the regression procedure. |
Value for constant term | constterm | If required, you can impose a value for the constant term which will be used to compute the coefficients. A value can be entered here if the Set value for constant term check box has been selected. |
P-value confidence | linfitconfpval | The p-value confidence value. |
Set value for constant term | If selected, you can enter a value in Value for constant term, which will be used to compute coefficients | |
Aggregate data before processing | aggregate | If selected, identical patterns are aggregated and considered as a single pattern during the training phase. |
Initialize random generator with seed | initrandom, iseed | If selected, a seed, which defines the starting point in the sequence, is used during random generation operations. Consequently using the same seed each time will make each execution reproducible. Otherwise, each execution of the same task (with same options) may produce dissimilar results due to different random numbers being generated in some phases of the process. |
Append results | append | If selected, the results of this computation are appended to the dataset, otherwise they replace the results of previous computations. |
Results
The results of the Linear task can be viewed in:
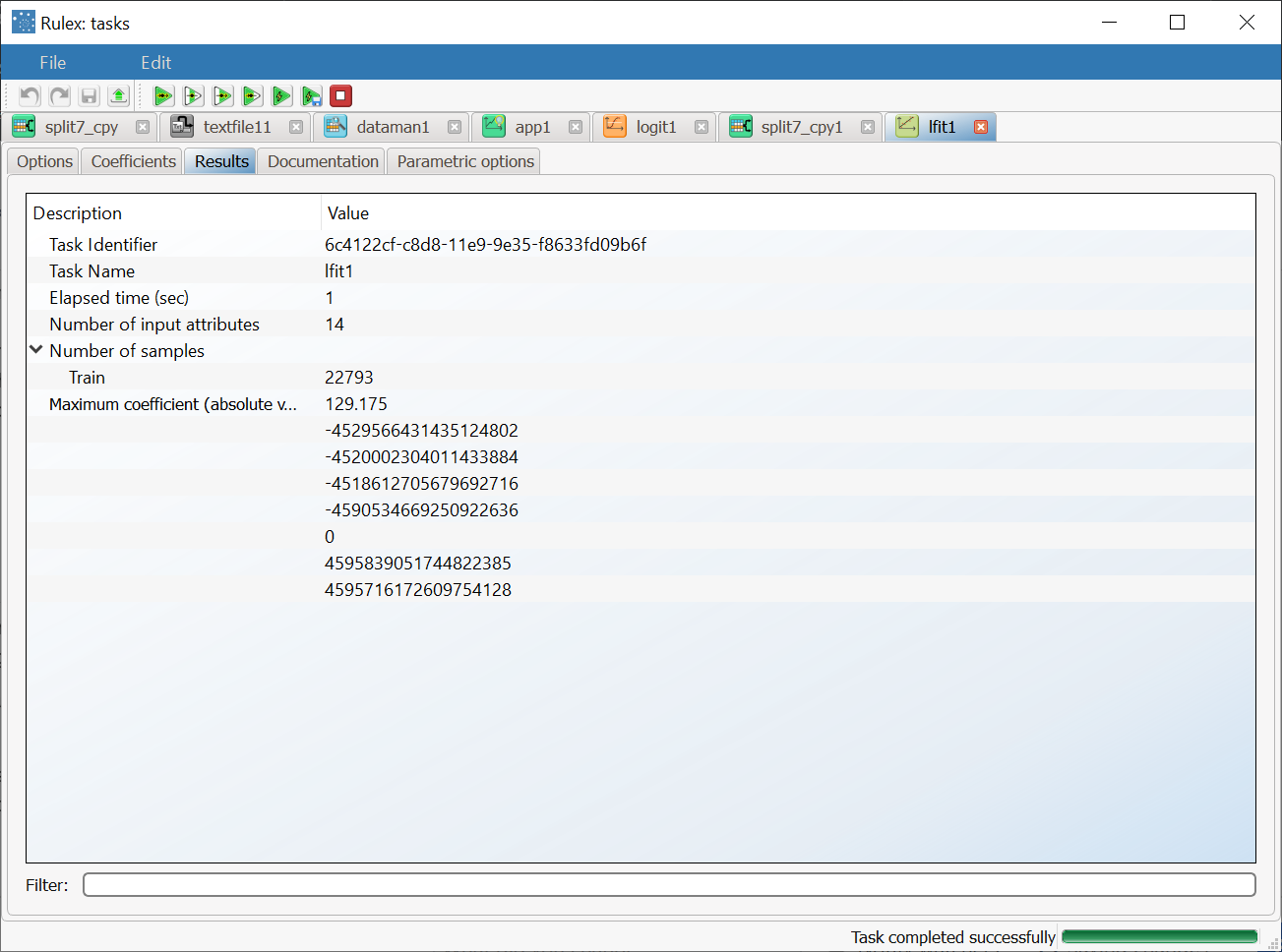
the Results tab, where statistics such as the execution time, number of attributes etc. are displayed.
the Coefficients tab, where the weight vector 𝓌1 relative to the Linear approximation is shown. Each element of the array is the coefficient of a single input attribute in the linear combination.
Example
The following examples are based on the Adult dataset.
Scenario data can be found in the Datasets folder in your Rulex installation.
The scenario aims to solve a simple regression problem based on the hours per week people statistically work, according to such factors as their age, occupation and marital status.
The following steps were performed:
First we import the adult dataset with an Import from Text File task.
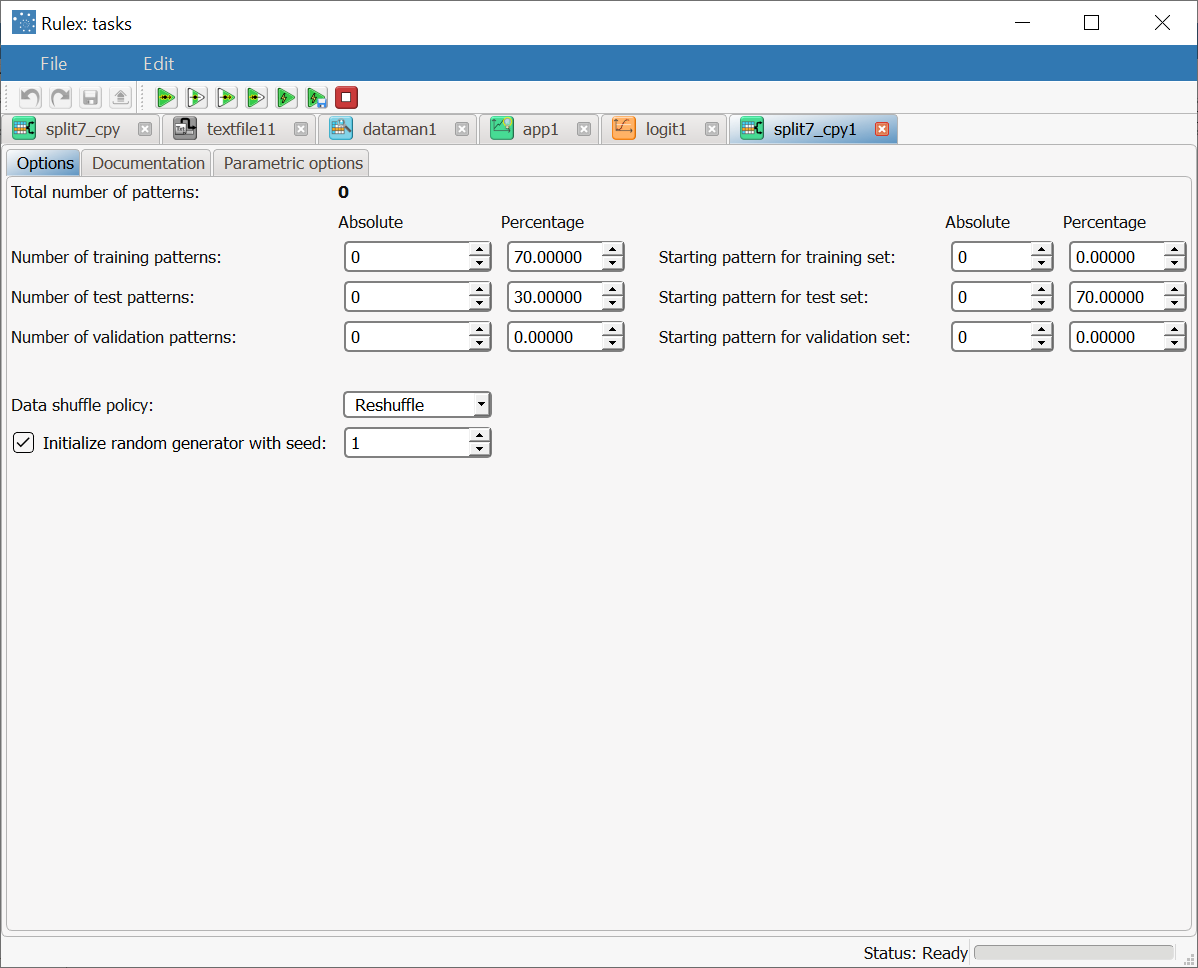
Split the dataset into a test and training set with a Split Data task.
Generate the model from the dataset with the Linear task.
Apply the model to the dataset with an Apply Model task, to forecast the output associated with each pattern of the dataset.
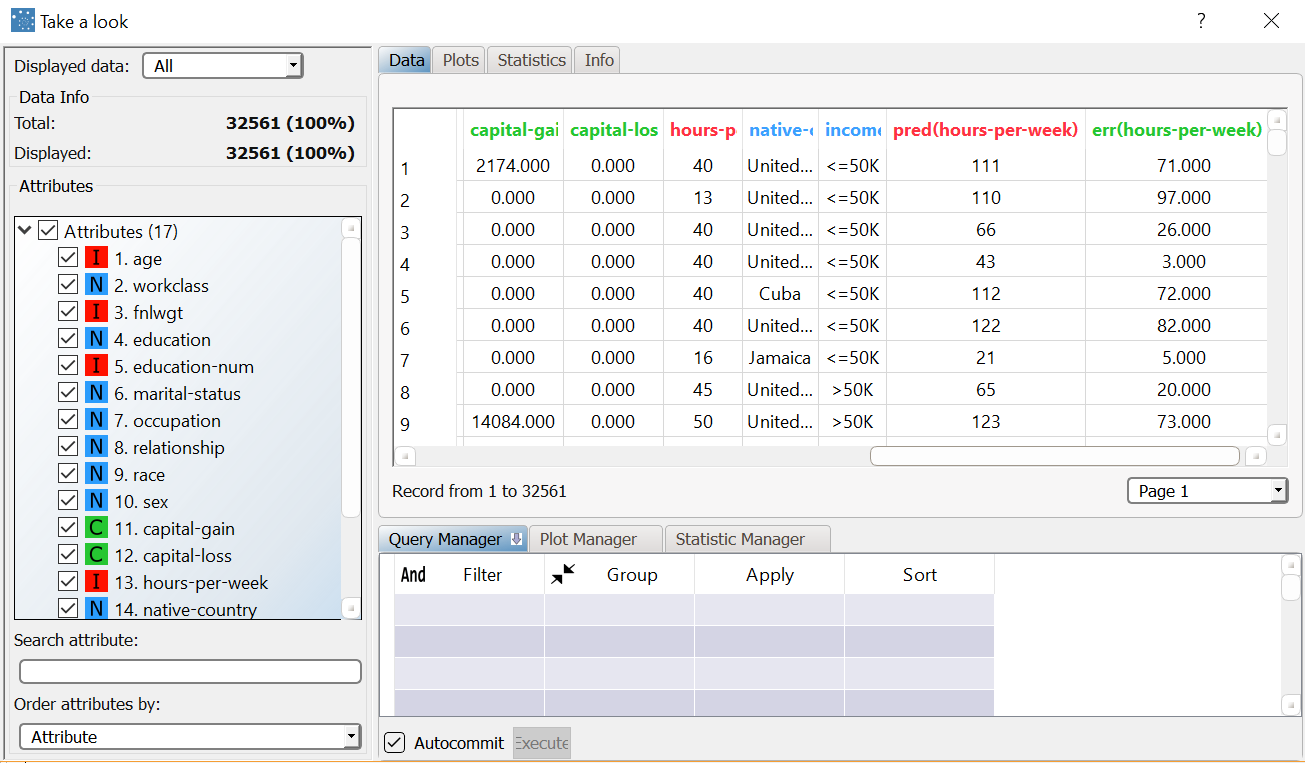
Use the Take a look functionality to view the results.
Procedure | Screenshot |
|---|---|
After importing the adult dataset with the Import from Text File task and splitting the dataset into test (30% of dataset) and training (70% of dataset) sets with the Split Data task, add a Linear task to the process and double click the task. | |
Leave default settings (no fixed value for the constant term) and drag and drop all attributes onto the Selected input attributes list except Income and hours-per-week. Drag and drop the hours-per-week attribute onto the Selected output attribute list. The dataset also contains nominal attributes, which in general cannot be handled by the OLS algorithm. In order to overcome this problem, the Linear task performs a continuization on these variables, which means that it turns them into ordered variables. | |
Once the computation has terminated we obtain a model which includes the weight vector 𝓌0,𝓌1,...,𝓌d. The Results tab contains a summary of the computation. Then add an Apply Model task to forecast the output associated with each pattern of the dataset. | |
To check how the model built by Linear has been applied to our dataset, right-click the Linear task and select Take a look. The Apply Model task has added two result columns:
|