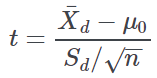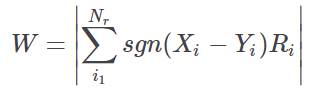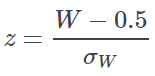Computing Statistics - Test for Paired Samples
Test for paired samples includes the two most common statistical tests for matched samples of a continuous attribute:
the Student t test
the Wilcoxon test variants for paired samples.
Paired samples include data measured twice on the same individual, for example before and after a medical treatment, or, slightly less frequently, data from different subjects sampled in a non-independent manner, for example on a pair of twins, one affected by a disease and the other selected as control.
Category | Properties | Description |
|---|---|---|
Sample size | Number of valid samples | The number of valid data samples for both attributes n is displayed. This is particularly useful when there is a heavily unbalanced distribution of missing data among the two attributes, which might cause the analysis to be based on an unacceptably small sample size. |
Student t-test | Student t-value and P-value for Student t-test | This test is used to assess the hypothesis that the difference between each couple under observation is zero. The corresponding test statistic is based on the ratio between the average of all differences and the corresponding standard error:
where |
Wilcoxon and Mann-Whitney test |
| This test is generally used instead of the Student t test when Xd is not Normally distributed. The test is distribution-free (“non-parametric”) being based on the ranks of Xd observed distribution. Ranks are the progressive numbers of the ordered values of a variable:
where Nr is the number of couples whose difference is not zero, and Ri is the rank of the i-th couple. Inference (i.e. the p-value calculation) is made by the following test:
z asymptotically follows a standard Normal distribution with standard error σW given by the following equation:
|
